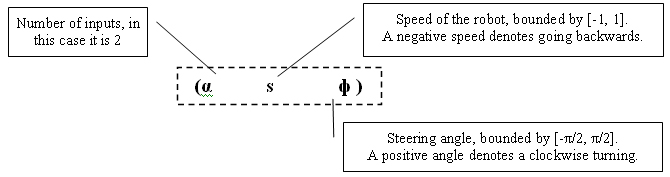
Descriptions of Input Vectors

The State Transition Equation for A Wheelchair in 2D Spaces

Let each state of the robot be represented as (x, y, ө), where (x, y) denotes the coordinates of the robot in a 2D configuration space, ө denotes the facing direction of the robot. Then we have the following State Transition Equation (also see Differential Models, Steven LaValle, 2001):

                x    =    s*cos ө

                y    =    s*sin ө

                ө    =    s/L*tan ф

Where 

                s —speed of the robot

                L—length of the robot

                ф—steering angle.

An input vector has a following format

Implementation

See model2d.cpp of Motion Strategy Library, line 326

MSLVector Model2DRigidCar::StateTransitionEquation

(const MSLVector &x, const MSLVector &u)

{

  MSLVector dx(3);

  dx[0] = u[0]*cos(x[2]);

  dx[1] = u[0]*sin(x[2]);

  dx[2] = u[0]*tan(u[1])/CarLength;

  return dx;

}

Examples

An input file

            2   1.0   0.0

            2   1.0   0.4

            2   1.0   -0.4

means that each state of the robot can derive three new states by applying the above State Transition Equations:

1.      going straight forward,

2.      making a right turn while going forward, and

3.      making a left turn while going forward.

If an initial state and a goal state are given, the path planning problem in fact is a search-tree problem:

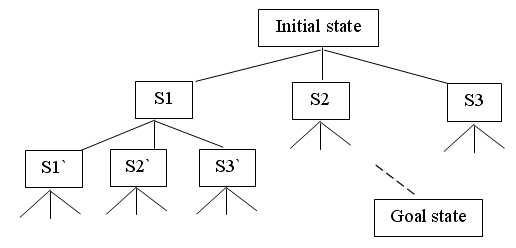
In Motion Strategy Library (MSL), this tree-like structure is the foundation for utilizing search strategies such as Rapidly-Exploring Random Trees (RRT) and A*.

Another Inputs file

2   1.0   0.0

2   1.0   0.1

2   1.0   -0.1

2   -1.0  0.0

2   -1.0  0.1

2   -1.0  -0.1

means that each state of the robot can derive six new states by applying the State Transition Equations:

1.      going straight forward,

2.      making a right turn while going forward,

3.      making a left turn while going forward,

4.      going straight backward,

5.      making a right turn while going backward, and

6.      making a left turn while going backward.

Important Highlights

·        Value of s (i.e., speed) can be any float number between -1.0 and 1.0. A vector (2, 0, 0.2) will enable a robot to rotate clockwise by 0.2 (rad) at the same position.

·    In the geometric description of a robot, (0, 0) denotes the middle point of the axle of the wheels, which also corresponds the position of the robot in a 2D configuration space.