Neural Networks are good at detecting hidden relations in a set of patterns (non-linear, many-to-many relations). Pythia is a program for the development and design of Neural Networks.
In this case, I just want to test whether this approach is effective or not: examine the Dow Jones Industrial Index, simply assume that there might be a relation between today’s open, high, low, close and volume and tomorrow’s close .(In fact, there might be more parameters like interest rates, overseas market indices, currency ratio etc. )
DJI open, high, low, close and volume in 1999
| Date | Open | High | Low | Close | Volume |
|---|---|---|---|---|---|
| 1/4/99 | 9184.01 | 9350.33 | 9122.47 | 9184.27 | 883 |
| 1/5/99 | 9184.78 | 9338.74 | 9182.98 | 9311.19 | 779 |
| 1/6/99 | 9315.42 | 9562.22 | 9315.42 | 9544.97 | 986 |
| 1/7/99 | 9542.14 | 9542.14 | 9426.02 | 9537.76 | 857 |
| 1/8/99 | 9538.28 | 9647.96 | 9525.41 | 9643.32 | 940 |
| 1/11/99 | 9643.32 | 9643.32 | 9532.61 | 9619.89 | 816 |
The basic idea is: to train a back propagation network with the data of first half 1999, then to "predict" second half (7-12).
- Just follow the example of Pythia manual: "Using the values directly as input into our network is not advisable because our interest is merely the percent drop and gain. We therefore derive our input data from the original data in the following way":
ΔOpen(t) = % change day t-1 -> day t = (Open(t)-Open(t-1))/Open(t-1)*100
ΔHigh(t) = % rel. to Open = (High(t)-Open(t))/Open(t)*100
ΔLow(t) = % rel. to Open = (Low(t)-Open(t))/Open(t)*100
ΔClose(t) = % change day t-1 -> day t = (Close(t)-Close(t-1))/Close(t-1)*100
ΔVolume(t) = % change day t-1 -> day t = (Volume(t)-Volume(t-1))/Volume(t-1)*100
The output we define as ΔClose(t+1) = % change day t -> day t+1 = (Close(t+1)-Close(t))/Close(t)*100 - Generating a good neural networks with Genetic Algorithm: that is to find a good networks topology suitable for this data.
- To train these neural networks with data of first half 1999.
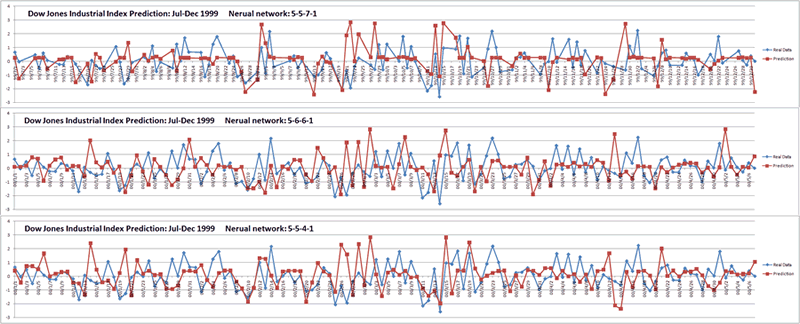
- Use trained neural networks to predict the second half of 1999, and here is the results. I think it's reasonable: the relations between today’s open, high, low, close and volume and tomorrow’s close dose exist, but not decisive. The most important thing is : this example proves that if we use neural networks appropriately, it will be really helpful.
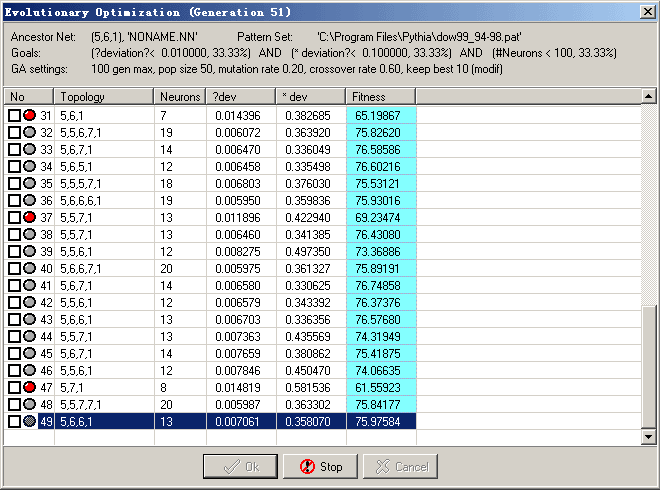
Then I found topology of 5-5-7-1, 5-6-6-1,and 5-5-4-1 have high fitness.
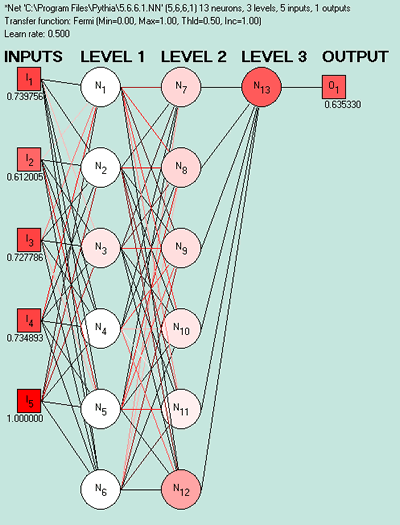
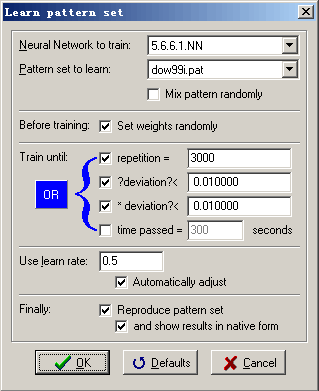
Training Neural Networks
Neural Network with topology of 5-6-6-1
"It must be stated clearly: No Neural Network can ever predict a market crash or any point gain or loss due to actual economical or political events you don’t know in advance. But a Neural Network might be able discover relations between stock market data that are not obvious."
VRP (Vehicle Routing Problem) is a well-known NP-Hard problem in the combinatorial optimization field. A typical vehicle routing problem can be described as the problem of designing least cost routes from one distribution center to a set of geographically scattered points (cities, stores, warehouses, schools, customers etc.).
For example, a distribution center (DC) locates at (145km,130km), and there are 20 customers, of which locations and demands of goods are in the following table. We have only 5 trucks, each truck is able to carry at most 8 ton goods and run as long as 500km at one time. Now the problem is: how to arrange the routs at least cost?
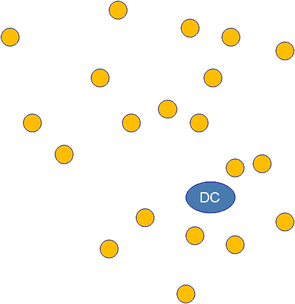
| Customer No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x (km) | 128 | 184 | 154 | 189 | 155 | 39 | 106 | 86 | 125 | 138 |
| y (km) | 85 | 34 | 166 | 152 | 116 | 106 | 76 | 84 | 21 | 52 |
| Demand(t) | 0.1 | 0.4 | 1.2 | 1.5 | 0.8 | 1.3 | 1.7 | 0.6 | 1.2 | 0.4 |
| Customer No. | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| x (km) | 67 | 148 | 18 | 171 | 74 | 2 | 119 | 132 | 64 | 96 |
| y (km) | 169 | 26 | 87 | 110 | 10 | 28 | 198 | 151 | 56 | 148 |
| Demand(t) | 0.9 | 1.3 | 1.3 | 1.9 | 1.7 | 1.1 | 1.5 | 1.6 | 1.7 | 1.5 |
There was a lot of fun with development of this program. By solving this problem with genetic algorithm, I can imagine I'm the god, creating many kinds of creatures, each stands for one solution. The following table shows 2 individuals, which contain routes information in their gene.
| No | ||||
|---|---|---|---|---|
| 1 | Gene | 12-10-2-9-5-14-20-3-4-18-17-16-8-19-7-11-6-13-15-1 | ||
| Routes | 0-12-10-2-9-5-14-20-0 | 0-3-4-18-17-0 | 0-16-8-19-7-0 | 0-11-6-13-15-1-0 | |||
| Total distance | 1593.6259765625 | Fitness | 0.000905653431905891 | |
| 1499 | Gene | 2-20-16-4-13-12-1-9-8-18-5-15-3-6-14-11-7-10-17-19 | ||
| Routes | 0-2-20-0 | 0-16-4-0 | 0-13-12-1-0 | 0-9-8-18-5-0 | 0-15-3-0 | 0-6-14-11-0 | 0-7-10-17-0 | 0-19-0 | |||
| Total distance | 2807.85594177246 | Fitness | 0.0005140124225665 | |
Then I created thousands of individuals, and set the rules: "survival of the fittest", better individuals have more change to have children. Besides, It's necessary to introduce new creatures at the beginning of each generation, and to let some individuals mutate. In this way premature convergence can be avoided.
The rest thing is to observe them "living" in the small world I created, and to get a satisfying solution at the end.
| Generation | Population | Least (km) | Average (km) |
|---|---|---|---|
| 0 | 2264 | 1596.66734427304 | 2197.55539580735 |
| 1 | 2042 | 1526.05910754587 | 2069.60841984751 |
| 2 | 1831 | 1526.05910754587 | 1990.58993605403 |
| 3 | 1648 | 1483.09592003891 | 1958.42372527935 |
| 4 | 1515 | 1483.09592003891 | 1932.0907494584 |
| 5 | 1465 | 1483.09592003891 | 1906.22481851749 |
| 6 | 1416 | 1325.13323413734 | 1864.15730162241 |
| 7 | 1444 | 1325.13323413734 | 1860.85415519988 |
| 8 | 1434 | 1325.13323413734 | 1839.7604002614 |
| 9 | 1380 | 1325.13323413734 | 1844.15417540795 |
| 10 | 1388 | 1325.13323413734 | 1814.33679019852 |
| 11 | 1345 | 1311.8305302498 | 1751.06987132262 |
| 12 | 1397 | 1295.14167082336 | 1756.29748418473 |
| 13 | 1349 | 1184.88285838633 | 1769.30937874342 |
| 14 | 1355 | 1184.88285838633 | 1767.97844578199 |
| 15 | 1347 | 1184.88285838633 | 1739.16548397984 |
| 16 | 1446 | 1184.88285838633 | 1749.44756231269 |
| 17 | 1474 | 1184.88285838633 | 1741.12932464921 |
| 18 | 1297 | 1184.88285838633 | 1698.10179191744 |
| 19 | 1229 | 1129.16889762462 | 1703.7091873959 |
| 20 | 1341 | 1129.16889762462 | 1700.72462627656 |
| 21 | 1355 | 1129.16889762462 | 1710.48802469976 |
| 22 | 1199 | 1108.66546638144 | 1653.74457310795 |
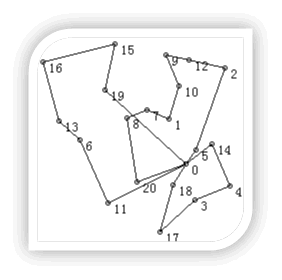
Solution with total distance of 1108.665 km
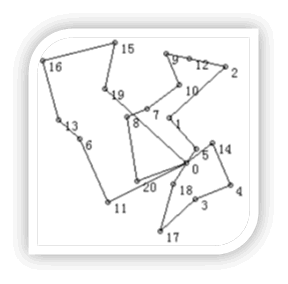
.png)
2 Solutions with total distance of 1112.9985 km